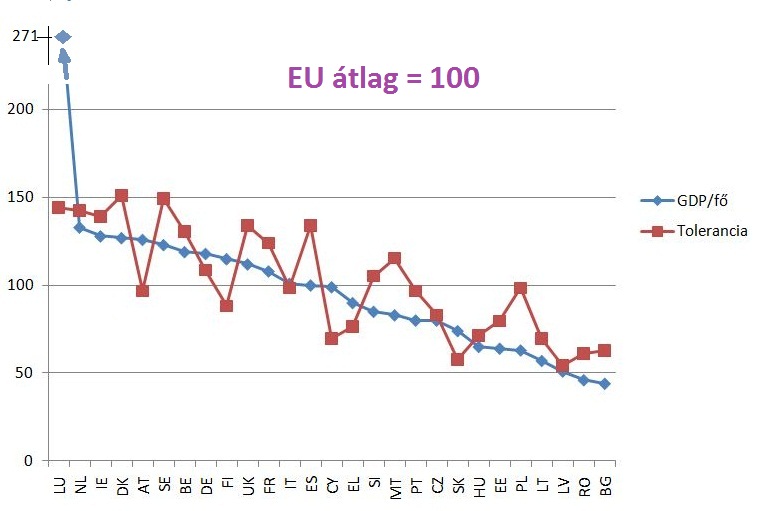
Az elmúlt napokban az Európai Bizottság közzétette az EU-n belüli diszkriminációról szóló legfrissebb tanulmányt. Sok egyéb érdekes adat mellett megtalálható benne a különböző kisebbségekhez tartozókkal szemben észlelhető társadalmi elfogadás, illetve elutasítás felmérésére irányuló vizsgálatok eredménye is. Ezek között szerepel az EU tagállamok polgárainak arra a kérdésre adott válaszait tartalmazó adatsor, hogy mennyire fogadná el, ha az ország legmagasabb választott politikai tisztségét egy meleg, leszbikus, vagy biszexuális (LMB) személy töltené be (ld. 41. oldal). A tanulmányban publikált adatsort felhasználva készítettük el a fenti grafikont, mely az egyes EU tagországok egy főre eső GDP-jének sorrendjében (forrás: Eurostat) mutatja egy LMB közösséghez tartozó első számú politikai vezető elfogadottságának, tolerancia szintjének alakulását az EU-s átlag százalékában. A grafikon önmagában is magáért beszél, hiszen a kisebb-nagyobb eltérések ellenére már ránézésre is egyértelműen látható, hogy az EU tagállamok egy főre eső GDP-je és a tolerancia szintje nagyon hasonló tendenciát mutat. Valószínűleg a széles közvélemény számára sem jelent ennek az összehasonlításnak az eredménye nagy meglepetést, mivel nyilván azok is tudják, hogy a fejlettebb gazdasággal, magasabb egy főre eső GDP-vel rendelkező nyugat-európai országokban magasabb a többségitől eltérő szexuális irányultsággal szembeni tolerancia, akik egyébként nem értenek egyet azzal, ha ezt egy közszereplő nyíltan vállalja, és sosem szavaznának bizalmat olyan politikusnak, aki ezt megteszi.
Tekintettel arra, hogy az egyes országok esetében előfordulnak a grafikonon is látható tendenciáktól eltérő értékek, amelyeket – mint ellenpéldákat – lehet esetleg a két paraméter (a relatív egy főre jutó GDP és a felmérés adatai alapján meghatározott relatív tolerancia szint) közötti összefüggés cáfolataként értelmezni, ezért érdemes a matematikai statisztika módszereivel is elemezni az adatokat. Két adatsor közötti összefüggés elemzésére a reláció analízis módszerét szokták alkalmazni. Elvégezve a fenti adatokkal ezt a számítást az úgynevezett korrelációs együttható, az r=0,796-os értéket mutat (Luxemburg értékeinek figyelmen kívül hagyásával, a nyugati fejlett országok GDP-jéhez képest is kiugróan magas értéke miatt). A matematika statisztika szabályai szerint, ha az r>0,75-nél, akkor igen erős kapcsolat van a két változó között.
Az összefüggés tehát egyértelmű, és ha vannak is olyan országok, amelyek „kilógnak a sorból”, az adatok magukért beszélnek.
A következtetéseket mindenki levonhatja magának.
